The concept of PV and its relation to WV imagery
WV images show the amount of water vapor in the mid and upper troposphere. High values of humidity and condensed water droplets or ice crystals are represented by lighter shades of gray or white while dry zones are depicted as black stripes or dark areas.
Humidity in the upper levels of the troposphere stems from the ground or ocean surface and has been lifted up by dynamical processes like convection or large scale ascent. Dry zones in WV imagery result either from very dry air throughout the troposphere (e.g. air above large deserts), missing upward motion or the descent of dry stratospheric air masses. Hence, WV imagery reflects the vertical motion of air masses better than any other satellite channel.
The concept of potential vorticity helps us describe dynamic processes in the atmosphere. Apart from ascending and descending atmospheric flows, the concept of vorticity in an air parcel is of equal importance for understanding the dynamics of the troposphere. The concept of potential vorticity (PV) combines both.
When looking at the PV formula,
PV= - g( ζΘ + f) • δΘ/δp
two factors can be distinguished:
absolute vorticity (ζΘ + f)
and static stability (δΘ/δp).
It is important to note that the PV of an air parcel is conserved when the parcel moves along an isentropic surface on its way through the atmosphere. This is what it usually does, assuming we ignore diabatic processes and turbulent mixing. Under these presumptions, we can state that
PV=constant
for any air parcel in the upper troposphere.
Hence, when plotting the numerical field of PV superimposed on a WV image, PV is plotted with a constant value, for instance PV=1.5 (x10-6 m2 K kg-1) PV units [PVU], with isolbars reflecting the vertical coordinates of the PV=1.5 PVU surface (see figure 1).
Figure 1: WV 6.2 Ám channel from 1 February 2013 at 06:00 UTC. The magenta isolines depict the height of the PV=1.5 PVU surface in pressure coordinates [hPa].
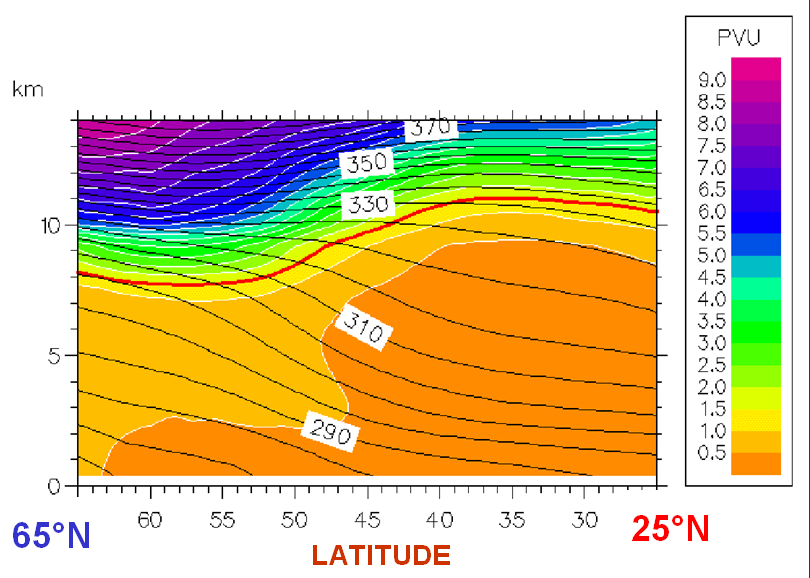
Why have we chosen the PV=1.5 PVU surface to be plotted on the WV image? One of the terms of potential vorticity is static stability. The stability of the atmosphere strongly increases when approaching the stratosphere (figure 2). In the troposphere, PV values ranging from 0.5 to 1 are quite common while in the stratosphere, PV mostly exceeds 3 PVU. The PV value 1.5 PVU has been chosen empirically to separate the stable stratosphere (PVU > 1.5.) from the less stable troposphere (PVU < 1.5). This is the so-called “dynamic tropopause”, not to be mixed with the thermodynamic definition of the tropopause, which is based on its vertical temperature gradient.
Figure 2: Vertical cross section of the troposphere. The black isolines depict equivalent potential temperature, while the different colors represent PV. The red line marks the PV=1.5 PVU surface (the dynamical tropopause).
Figure 1 can be interpreted as the height of the dynamical tropopause superimposed on a WV image. Black stripes and most dark zones located at the cold side of the polar front correspond to a low height of the PV=1.5 PVU surface. In these areas the dynamical tropopause reaches far into the troposphere and air parcels with high PV values protrude from higher into lower atmospheric levels (so-called stratospheric intrusion). Note that the PV value of an air parcel is constant along its way through the troposphere on an isentropic surface. These regions mark areas of subsidence and are referred to as “dynamic tropopause anomaly” or simpler “PV anomaly”.
Another aspect resulting from the conservation of PV affects the vorticity of the air parcel when static stability changes. Due to the reciprocity of static stability and absolute vorticity with PV=const., if one term increases, the other decreases accordingly.
Figure 3: Illustrates how the vorticity of an air parcel increases, when static stability decreases.
When stable stratospheric air masses are protruding down into the troposphere, the air parcels enter regions with less static stability (see figure 3). As a result of conservation of PV, the vorticity of the air parcel must increase. This phenomenon is often observed in cases of cyclogenesis and will be dealt with in more detail later in this module (see chapter 3). Diabatic processes such as the release of latent heat, friction and radiation can counteract the generation of vorticity in PV anomalies and lead to the disappearance of the anomaly.